动态规划一直是算法中比较难的一个,我认为原因有两个:一是动态规划很容易和分治法混淆,二是动态规划的算法比较难以理解,要一步步地优化,最优的动态规划算法难以直接构想出来,只有很熟悉才能做到。下面就从动态规划的定义与三个步骤入手,让动态规划更好理解。
什么是动态规划
动态规划解决的问题是可以分为多个不一定相互独立的子问题的。与动态规划相似,分治法解决的问题是可以分为多个相互独立的子问题的。这里的相互独立是什么意思呢?看下面两张图就明白了:
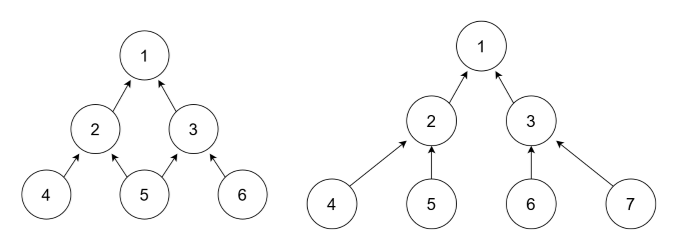
这里这两张图片里的树就代表了对问题的分解,根节点对应的问题是可以通过解决其直接子节点对应的问题来得到解的。例如两张图中的问题 1 都可以通过解决子问题 2 和 3 来得到它的解。我们可以看到两张图的不同之处在于左边的图中解决子问题 5 不单单可以解决问题 2, 还可以解决问题 3,而右图中所有子问题只对应一个父问题。如左图中子问题 5 就不是问题 2 和 3 的独立子问题,而右图中所有子问题都是独立的。而动态规划解决的问题都是左图的问题,分治法解决的是右图的问题。
第一步:分治法
可以分解成若干个子问题的问题,最直观的解法就是分治法了。动态规划也是一样,我们先用分治法来解决了这个问题,再去考虑如何优化算法。这里就以上面的左图为例,用分治法解决的分解大致如下:
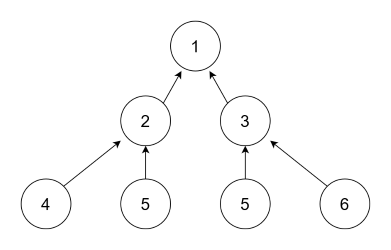
就如同分治法解决的问题一样,分治法本身每一步水平之间都是独立的,互相之间没有任何交流,所以在解决问题 2 和问题 3 时都要独立地解决一遍问题 5,这里就给我们下一步留下了优化的空间。
第二步:空间换时间
正如上一步骤所说,使用分治法解决这种子问题不相互独立的问题会出现反复求解同一子问题的现象。这时就可以通过空间换时间来优化了,把每个子问题求解得到的结果储存起来,到下一次用的时候直接调用就行了。这里就是用储存答案的空间换取部分解非独立子问题所需的时间。大致的解决步骤如下,方框代表的是储存起来的问题的解:
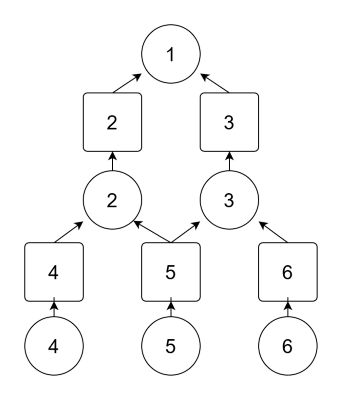
虽然看起来我们这只节省了计算一个子问题 5 的时间,却多加了对 5 个问题解的存储空间,但是当这个问题树扩展起来时,一个不独立的子问题的解可能是要计算许多的其它子问题来获得的,这些不独立子问题的子问题也要重新计算,这时把计算结果储存起来带来的算力节约就很明显了。
第三步:压缩空间
在用空间换时间后,我们也要考虑一下内存有没有优化的空间。一层层地看这颗树,每一层的问题只需要下一层的问题的解即可,而下下层是没有用的。例如图中的问题 1,只需要问题 2 和问题 3 的解,问题 4、5、6是没有用的。所以我们在内存中只需要存储一层的问题解就可以了,不需要存储所有问题的解。
练习一下
了解了动态规划优化的步骤,要练习一下才能融会贯通。这里就举一个力扣的问题:70.爬楼梯,来应用这上述的方法。
假设你正在爬楼梯。需要
n阶你才能到达楼顶。 每次你可以爬1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?
这个问题的解题步数会随着 n 的变化而变化,为了方便表示,我们可以将爬上 n 阶楼题的不同方法的解用 G(n) 表示。解 G(n) 与解 G(n-1) 本质上是一样的,可以套用同一个函数解,从而把问题分解为更为容易解决的小规模子问题。但光是可以分解为小规模子问题还不能用分治法解,还需能用规模较小的子问题的解合并得出规模较大的子问题的解。爬到 n 阶就只有两种可能,一是从 n-1 阶爬 1 阶,二是从 n-2 阶爬 2 阶,所以说 G(n) 可以由 G(n-1) 和 G(n-2) 这两个子问题的解合并而成,直接相加就可以了。这个问题不断分解就分解到爬到 1 阶的问题和爬到 2 阶的问题这两个问题了,它们的解分别是 1 和 2,也是规模足够小可以人脑推出来的。这样就完成了第一步,Python 代码如下:
class Solution:
def climbStairs(self, n: int) -> int:
if n == 1:
return 1
elif n == 2:
return 2
else:
return self.climbStairs(n-1) + self.climbStairs(n-2)
但是当阶数大起来的时候,这种分治法重复运算子问题耗时大,也过不了力扣的时间限制。于是得要用第二步优化时间复杂度,用空间换时间,加入一个数组储存问题的答案。
class Solution:
answer = [1, 2] # 索引为 n 则为 爬 n+1 阶楼梯的解
def climbStairs(self, n: int) -> int:
if len(self.answer) < n:
self.answer.append(self.climbStairs(n-1) + self.climbStairs(n-2))
return self.answer[n-1]
这样子就可以通过力扣的时间限制了,只不过这里的内存消耗 15 MB,连一半的用户都没超过,内存还有优化的空间。
第三步,优化内存占用,最关键的就是找到问题与其子问题之间的关系,我们在第一步就已经解析出来了,假设 n 阶问题的解为 G(n),则有状态转移方程:
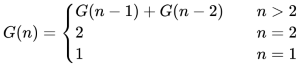
从状态转移方程可以看出,只需要保存两个解,就可以解出下一个解了,不需要把所有问题的解都保存。下面就是第三步优化后的代码:
class Solution:
def climbStairs(self, n: int) -> int:
if n < 3:
return n
x, y = 1, 2
for _ in range(3, n + 1):
x, y = y, x + y
return y
这样就完成了动态规划的三个步骤。当然,动态规划问题比较灵活多变,这三个步骤只是针对比较典型的动态规划问题,有一些动态规划问题中可能会出现部分步骤不适用或是没有优化空间的情况,还望读者灵活应用。